ソリューションReezoteのSEO支援

SEOに関してはそのロジックに諸説あるのはみなさんご存知の通りです。

弊社のSEOはベトナムの関連会社であるSEO研究機関のデータに基づいています。

SEOがいくら複雑とはいえ、数学モデルにしてしまうことは可能です。

なぜなら

SEO評価は所詮は複数の評価項があり
その項にそれぞれ係数があり、
その項同士は演算子で計算されていて
そのような式群が複数ありますが、
特定の条件でどこかの式群を見るように分岐されている
その合計値のスコアを算出する

このような抽象的な式で表すことができます。

この抽象的な式を表現するためには、式群ごとの項、係数、演算子、条件による分岐、そして最終的な合計値のスコアを算出する全体のフレームワークが必要です。以下はその概念をモデル化した式です：

前提：

• それぞれの式群は、項 (x_1, x_2, \dots, x_n) と係数 (a_1, a_2, \dots, a_n) で構成される。
• 演算子は加算、減算、掛け算、または他の演算子（例：累乗など）を含む可能性がある。
• 条件に基づいて、複数の式群のうちどれを選択するかが決まる。

抽象的な表現：

各式群の表現：

式群 (E_k)（(k)は式群の番号）は次のように定義されるとする：

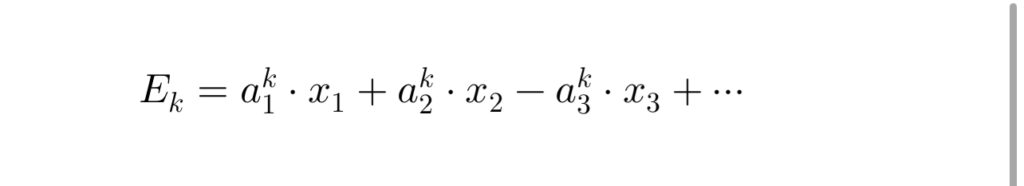
条件による分岐：

式群 (E_k) の選択は、条件 (C_1, C_2, \dots, C_m) によって分岐する。この条件を満たす式群が選択されるとする：

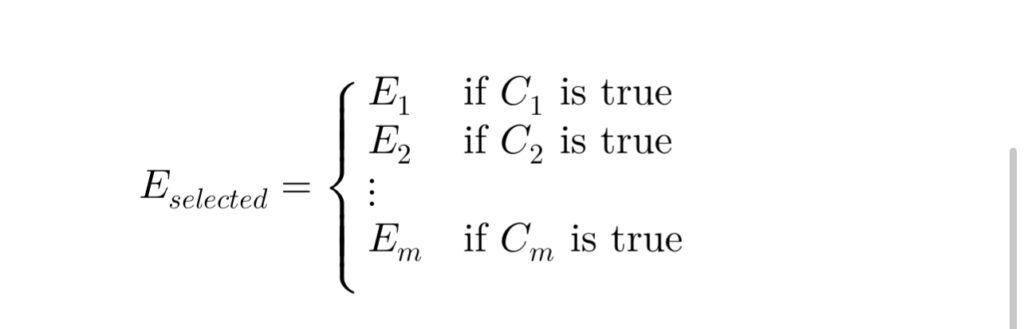
最終的なスコアの算出：

選択された式群 (E_{selected}) に基づいて、合計スコア (S) を次のように計算する：

[S = E_{selected}]

具体例：

例えば、次のような式群があった場合：

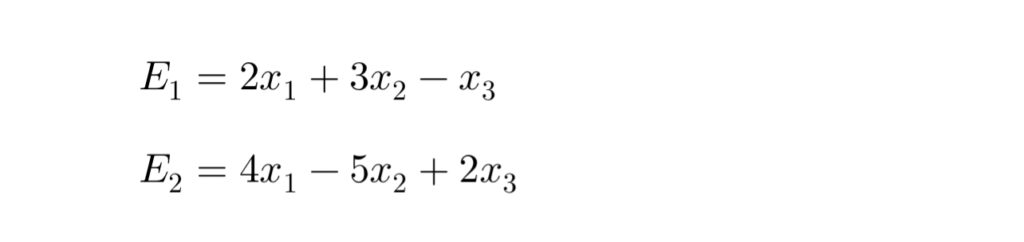
そして、条件 (C_1) と (C_2) に基づいて式群 (E_1) または (E_2) が選ばれ、最終スコアが計算される。

このようなモデルに基づいて、特定の係数、項、演算子、条件を使って複雑なスコアリングシステムを構築することができます。

一つの式で表すと

一つの式での表現：

複数の式群 (E_1, E_2, \dots, E_m) と、それに対応する条件 (C_1, C_2, \dots, C_m) を用いて、以下のように表現できます。

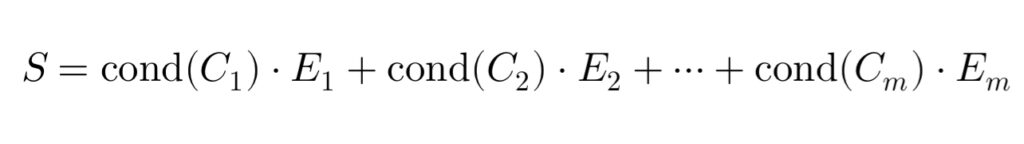
この項の種別と係数、そしてどの条件でどちらの式に行くのか、そのスコアの合計値、これがSEOの評価ロジックであることは確実です。

これはデカルト的に断言できます。

これらを研究するには年間数千万円のコストがかかりますが、これは弊社の関連会社に任せ、結末だけをコンサルさせていただければ効率は良いですね。

どのサイトでも確実に順位をあげ、なぜ上がるのかも明確に説明できます。